Intermediate Value Theorem
To begin with, let’s start with the basic statement of the theorem.
Theorem
If \(f(x)\) is continuous on a closed interval \([a,b]\) and \(N\) is any number \(f(a) < N < f(b)\) then there exists a value \(c \in (a,b)\) such \(f(c) = N\).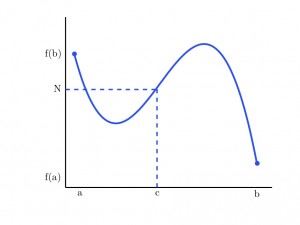
The illustration corresponding to the theorem is to the right and indicates that there may be more than one possible value for \(c\). The important restrictions are that
- \(f(x)\) be continuous and
- the interval \([a,b]\) is closed.
The primary purpose of this theorem is to indicate when numbers with various properties exist.
Steps
1. Make sure the function, \(f(x)\) is continuous.
2. Create a new function \(g(x)=f(x)-N\), replacing the function in this manner always makes the \(N\) in the theorem with respect to \(g\) equal to zero. So that \(g(c)=0\) when a correct value for \(c\) is determined.
3. Using 0 rather than the general \(N\), we need to find an \(a\) and a \(b\) so that either \(g(a)>0\) and \(g(b)<0\) or \(g(a)<0\) and \(g(b)>0\). The point is that the signs need to change.
4. Finding a change of sign confirms that there is a number \(c \in (a,b)\) that allows \(g(c)=0\) or \(f(c)=N\).
Examples
A. Suppose we have the function \(f(x) = x^2 – 4x\) and we wish to show there is a number \(x_*\) such that \(f(x_*) = 1\).
1. Notice that since \(f(x)\) is continuous, the intermediate value theorem can be used.
2. Let \(g(x) = f(x) – 1 = x^2 – 4x – 1\) so that \(g(x) = 0\) when the correct \(x_*\) is determined.
3. Choosing \(a = 4\) gives \(g(a) = -1 < 0\) and choosing \(b=5\) gives \(g(b) = 4 > 0\). There are of course many other possible value of \(a\) and \(b\). Note that \(a<b\).
4. Since a change in sign was found, there is a number \(c \in (4,5)\) such that \(g(c) = 0\) or equivalently, \(f(c) = 1\).
B. If \(f(x) = x^3-8x+10\), show there is at least one value of \(c\) for which \(f(c) = -\sqrt{3}\).
Since \(f(x)\) is continuous we just need to redefine the function (to make \(N = 0\)) and find values for \(a\) and \(b\). The new function is
\[
g(x) = f(x) + \sqrt{3} = x^3-8x+10+\sqrt{3}.
\]
We need to find \(a\) and \(b\) so that \(g(x)\) changes sign. Let \(a=-4\) so that \(f(a) = -22+\sqrt{3} < 0\) and \(b=-3\) so that \(f(b) = 7+\sqrt{3} >0\). These choices for \(a\) and \(b\) are found by just trying different values in the function.
At any rate, using the intermediate value theorem we can conclude that there is a value \(c \in (-4,-3)\) such that \(g(c) = 0\) or \(f(c) = -\sqrt{3}\).
Hi Sean,
I ran across this while scooping UOIT’s Math grad website.
I’m not so convinced about the -N traslation of the function f and it’s purpose. The IVT is basically equivalent to Dedekind completeness (or LUB property ) of the reals. Your reasoning “work” for over the rationals too (because in a sense, they look “complete” when you graph functions over the rationals). And the -N seems unnecessary too.
Thanks